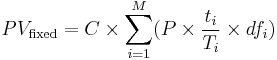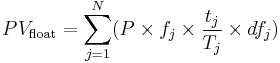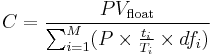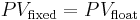Interest rate swap
An interest rate swap is a popular and highly liquid financial derivative instrument in which two parties agree to exchange interest rate cash flows, based on a specified notional amount from a fixed rate to a floating rate (or vice versa) or from one floating rate to another.[1] Interest rate swaps are commonly used for both hedging and speculating.
Contents |
Structure
In an interest rate swap, each counterparty agrees to pay either a fixed or floating rate denominated in a particular currency to the other counterparty. The fixed or floating rate is multiplied by a notional principal amount (say, USD 1 million). This notional amount is typically not exchanged between counterparties, but is used only for calculating the size of cashflows to be exchanged.
The most common interest rate swap is one where one counterparty A pays a fixed rate (the swap rate) to counterparty B, while receiving a floating rate indexed to a reference rate (such as LIBOR). By market convention, the counterparty paying the fixed rate is called the "payer" (while receiving the floating rate), and the counterparty receiving the fixed rate is called the "receiver" (while paying the floating rate).
A pays fixed rate to B (A receives variable rate)
B pays floating rate to A (B receives fixed rate)
Currently, A borrows from Market @ LIBOR +1.5%. B borrows from Market @ 8.5%.
Consider the following swap in which Party A agrees to pay Party B periodic fixed interest rate payments of 8.65%, in exchange for periodic variable interest rate payments of LIBOR + 70 bps (0.70%). Note that there is no exchange of the principal amounts and that the interest rates are on a "notional" (i.e. imaginary) principal amount. Also note that the interest payments are settled in net (e.g. Party A pays (LIBOR + 1.50%)+8.65% - (LIBOR+0.70%) = 9.45% net). The fixed rate (8.65% in this example) is referred to as the swap rate.[2]
At the point of initiation of the swap, the swap is priced so that it has a net present value of zero. If one party wants to pay 50 bps above the par swap rate, the other party has to pay approximately 50 bps over LIBOR to compensate for this.
Types
Being OTC instruments, interest rate swaps can come in a huge number of varieties and can be structured to meet the specific needs of the counterparties. For example, the legs of the swap can be in the same currency or in different currencies. The notional of the swap could be amortized over time. The reset dates of the floating rate could be non-regular, etc. However, in the interbank market, just a few, standardized types are traded. They are listed below.
Fixed-for-floating rate swap, same currency
Party B pays/receives fixed interest in currency A to receive/pay floating rate in currency A indexed to X on a notional amount N for a term of T years. For example, you pay fixed 5.32% monthly to receive USD 1M Libor monthly on a notional USD 1 million for 3 years. The party that pays fixed and receives floating coupon rates is said to be long the interest swap because it is expressed as a bond convention (as prices fall, yields rise). The party interested to pay fixed and receive floating is bullish on interest rate and so long his position and thus, buy floating rate. Interest rate swaps are simply the exchange of one set of cash flows for another.
Fixed-for-floating swaps in same currency are used to convert a fixed rate asset/liability to a floating rate asset/liability or vice versa. For example, if a company has a fixed rate USD 10 million loan at 5.3% paid monthly and a floating rate investment of USD 10 million that returns USD 1M Libor +25 bps monthly, it may enter into a fixed-for-floating swap. In this swap, the company would pay a floating rate of USD 1M Libor+25 bps and receive a 5.5% fixed rate, locking in 20bps profit.
Fixed-for-floating rate swap, different currencies
Party P pays/receives fixed interest in currency A to receive/pay floating rate in currency B indeed to X on a notional N at an initial exchange rate of FX for a tenure of T years. For example, you pay fixed 5.32% on the USD notional 10 million quarterly to receive JPY 3M (TIBOR) monthly on a JPY notional 1.2 billion (at an initial exchange rate of USD/JPY 120) for 3 years. For nondeliverable swaps, the USD equivalent of JPY interest will be paid/received (according to the FX rate on the FX fixing date for the interest payment day). No initial exchange of the notional amount occurs unless the Fx fixing date and the swap start date fall in the future.
Fixed-for-floating swaps in different currencies are used to convert a fixed rate asset/liability in one currency to a floating rate asset/liability in a different currency, or vice versa. For example, if a company has a fixed rate USD 10 million loan at 5.3% paid monthly and a floating rate investment of JPY 1.2 billion that returns JPY 1M Libor +50 bps monthly, and wants to lock in the profit in USD as they expect the JPY 1M Libor to go down or USDJPY to go up (JPY depreciate against USD), then they may enter into a Fixed-Floating swap in different currency where the company pays floating JPY 1M Libor+50 bps and receives 5.6% fixed rate, locking in 30bps profit against the interest rate and the fx exposure.
Floating-for-floating rate swap, same currency
Party P pays/receives floating interest in currency A Indexed to X to receive/pay floating rate in currency A indexed to Y on a notional N for a tenure of T years. For example, you pay JPY 1M LIBOR monthly to receive JPY 1M TIBOR monthly on a notional JPY 1 billion for 3 years.
Floating-for-floating rate swaps are used to hedge against or speculate on the spread between the two indexes widening or narrowing. For example, if a company has a floating rate loan at JPY 1M LIBOR and the company has an investment that returns JPY 1M TIBOR + 30 bps and currently the JPY 1M TIBOR = JPY 1M LIBOR + 10bps. At the moment, this company has a net profit of 40 bps. If the company thinks JPY 1M TIBOR is going to come down (relative to the LIBOR) or JPY 1M LIBOR is going to increase in the future (relative to the TIBOR) and wants to insulate from this risk, they can enter into a float-float swap in same currency where they pay, say, JPY TIBOR + 30 bps and receive JPY LIBOR + 35 bps. With this, they have effectively locked in a 35 bps profit instead of running with a current 40 bps gain and index risk. The 5 bps difference (w.r.t. the current rate difference) comes from the swap cost which includes the market expectations of the future rate difference between these two indices and the bid/offer spread which is the swap commission for the swap dealer.
Floating-for-floating rate swaps are also seen where both sides reference the same index, but on different payment dates, or use different business day conventions. This can be vital for asset-liability management. An example would be swapping 3M LIBOR being paid with prior non-business day convention, quarterly on JAJO (i.e. Jan, Apr, Jul, Oct) 30, into FMAN (i.e. Feb, May, Aug, Nov) 28 modified following・
Floating-for-floating rate swap, different currencies
Party P pays/receives floating interest in currency A indexed to X to receive/pay floating rate in currency B indexed to Y on a notional N at an initial exchange rate of FX for a tenure of T years. For example, you pay floating USD 1M LIBOR on the USD notional 10 million quarterly to receive JPY 3M TIBOR monthly on a JPY notional 1.2 billion (at an initial exchange rate of USDJPY 120) for 4 years.
To explain the use of this type of swap, consider a US company operating in Japan. To fund their Japanese growth, they need JPY 10 billion. The easiest option for the company is to issue debt in Japan. As the company might be new in the Japanese market without a well known reputation among the Japanese investors, this can be an expensive option. Added on top of this, the company might not have appropriate debt issuance program in Japan and they might lack sophisticated treasury operation in Japan. To overcome the above problems, it can issue USD debt and convert to JPY in the FX market. Although this option solves the first problem, it introduces two new risks to the company:
- FX risk. If this USDJPY spot goes up at the maturity of the debt, then when the company converts the JPY to USD to pay back its matured debt, it receives less USD and suffers a loss.
- USD and JPY interest rate risk. If the JPY rates come down, the return on the investment in Japan might go down and this introduces an interest rate risk component.
The first exposure in the above can be hedged using long dated FX forward contracts but this introduces a new risk where the implied rate from the FX spot and the FX forward is a fixed rate but the JPY investment returns a floating rate. Although there are several alternatives to hedge both the exposures effectively without introducing new risks, the easiest and the most cost effective alternative would be to use a floating-for-floating swap in different currencies. In this,
Fixed-for-fixed rate swap, different currencies
Party P pays/receives fixed interest in currency A to receive/pay fixed rate in currency B for a term of T years. For example, you pay JPY 1.6% on a JPY notional of 1.2 billion and receive USD 5.36% on the USD equivalent notional of 10 million at an initial exchange rate of USDJPY 120.
Other variations
A number of other variations are possible, although far less common. Mostly tweaks are made to ensure that a bond is hedged "perfectly", so that all the interest payments received are exactly offset by the swap. This can lead to swaps where principal is paid on one or more legs, rather than just interest (for example to hedge a coupon strip), or where the balance of the swap is automatically adjusted to match that of a prepaying bond (such as RMBS Residential mortgage-backed security)
Uses
Interest rate swaps were originally created to allow multi-national companies to evade exchange controls. Today, interest rate swaps are used to hedge against or speculate on changes in interest rates.
Speculation
Interest rate swaps are also used speculatively by hedge funds or other investors who expect a change in interest rates or the relationships between them. Traditionally, fixed income investors who expected rates to fall would purchase cash bonds, whose value increased as rates fell. Today, investors with a similar view could enter a floating-for-fixed interest rate swap; as rates fall, investors would pay a lower floating rate in exchange for the same fixed rate.
Interest rate swaps are also very popular due to the arbitrage opportunities they provide. Due to varying levels of creditworthiness in companies, there is often a positive quality spread differential which allows both parties to benefit from an interest rate swap.
The interest rate swap market is closely linked to the Eurodollar futures market which trades at the Chicago Mercantile Exchange.
British local authorities
In June 1988 the Audit Commission was tipped off by someone working on the swaps desk of Goldman Sachs that the London Borough of Hammersmith and Fulham had a massive exposure to interest rate swaps. When the commission contacted the council, the chief executive told them not to worry as "everybody knows that interest rates are going to fall"; the treasurer thought the interest rate swaps were a 'nice little earner'. The controller of the commission, Howard Davies realised that the council had put all of its positions on interest rates going down; he sent a team in to investigate.
By January 1989 the commission obtained legal opinions from two Queen's Counsel. Although they did not agree, the commission preferred the opinion which made it ultra vires for councils to engage in interest rate swaps. Moreover interest rates had gone up from 8% to 15%. The auditor and the commission then went to court and had the contracts declared illegal (appeals all the way up to the House of Lords failed); the five banks involved lost millions of pounds. Many other local authorities had been engaging in interest rate swaps in the 1980s, although Hammersmith was unusual in betting all one way.[3]
Valuation and pricing
The present value of a plain vanilla (i.e. fixed rate for floating rate) swap can easily be computed using standard methods of determining the present value (PV) of the fixed leg and the floating leg.
The value of the fixed leg is given by the present value of the fixed coupon payments known at the start of the swap, i.e.
where C is the swap rate, M is the number of fixed payments, P is the notional amount, ti is the number of days in period i, Ti is the basis according to the day count convention and dfi is the discount factor.
Similarly, the value of the floating leg is given by the present value of the floating coupon payments determined at the agreed dates of each payment. However, at the start of the swap, only the actual payment rates of the fixed leg are known in the future, whereas the forward rates (derived from the yield curve) are used to approximate the floating rates. Each variable rate payment is calculated based on the forward rate for each respective payment date. Using these interest rates leads to a series of cash flows. Each cash flow is discounted by the zero-coupon rate for the date of the payment; this is also sourced from the yield curve data available from the market. Zero-coupon rates are used because these rates are for bonds which pay only one cash flow. The interest rate swap is therefore treated like a series of zero-coupon bonds. Thus, the value of the floating leg is given by the following:
where N is the number of floating payments, fj is the forward rate, P is the notional amount, tj is the number of days in period j, Tj is the basis according to the day count convention and dfj is the discount factor. The discount factor always starts with 1. The discount factor is found as follows:
- [Discount factor in the previous period]/[1 + (Forward rate of the floating underlying asset in the previous period × Number of days in period/360)].
(Depending on the currency, the denominator is 365 instead of 360; e.g. for GBP.)
The fixed rate offered in the swap is the rate which values the fixed rates payments at the same PV as the variable rate payments using today's forward rates, i.e.:
Therefore, at the time the contract is entered into, there is no advantage to either party, i.e.,
Thus, the swap requires no upfront payment from either party.
During the life of the swap, the same valuation technique is used, but since, over time, the forward rates change, the PV of the variable-rate part of the swap will deviate from the unchangeable fixed-rate side of the swap. Therefore, the swap will be an asset to one party and a liability to the other. The way these changes in value are reported is the subject of IAS 39 for jurisdictions following IFRS, and FAS 133 for U.S. GAAP. Swaps are marked to market by debt security traders to visualize their inventory at a certain time.
Risks
Interest rate swaps expose users to interest rate risk and credit risk.
- Market Risk: A typical swap consists of two legs, one fixed, the other floating. The risks of these two component will naturally differ. Newcomers to market finance may think that the risky component is the floating leg, since the underlying interest rate floats, and hence, is unknown. This first impression is wrong. The risky component is in fact the fixed leg and it is very easy to see why this is so.
The discussion of pricing interest rate swaps illustrated an important point. Regardless of what happens to future Libor rates, the value of a rolling deposit or FRN always equals the notional amount N at the reset dates. Between the reset dates this value may be different than N, but the discrepancy cannot be very large since the δ will be 3 or 6 months. Interest rate fluctuations have minimal effect on the values of fixed instruments with such maturities. In other words, the value of the floating leg changes very little during the life of a swap.
On the other hand the fixed leg of a swap is equivalent to a coupon bond and fluctuations of the swap rate may have major effects on the value of the future fixed payments.
- Credit risk on the swap comes into play if the swap is in the money or not. If one of the parties is in the money, then that party faces credit risk of possible default by another party.
Market size
The Bank for International Settlements reports that interest rate swaps are the largest component of the global OTC derivative market. The notional amount outstanding as of June 2009 in OTC interest rate swaps was $342 trillion, up from $310 trillion in Dec 2007. The gross market value was $13.9 trillion in June 2009, up from $6.2 trillion in Dec 2007.
Interest rate swaps can now be traded as an Index through the FTSE MTIRS Index.
References
- ^ "Interest Rate Swap". Glossary. ISDA. http://www2.isda.org/functional-areas/research/Glossary#i.
- ^ "Interest Rate Swap" by Fiona Maclachlan, The Wolfram Demonstrations Project.
- ^ Duncan Campbell-Smith, "Follow the Money: The Audit Commission, Public Money, and the Management of Public Services 1983-2008", Allen Lane, 2008, chapter 6 passim.
- ^ "Understanding interest rate swap math & pricing". California Debt and Investment Advisory Commission. 2007-01. http://treasurer.ca.gov/CDIAC/publications/math.pdf. Retrieved 2007-09-27.
- Pricing and Hedging Swaps, Miron P. & Swannell P., Euromoney books 1991
See also
- Swap rate
- Interest rate cap and floor
- Equity swap
- Total return swap
- Inflation derivatives
- Eurodollar
- Constant maturity swap
- FTSE MTIRS Index
External links
- Bank for International Settlements - Semiannual OTC derivatives statistics
- Investopedia - Spreadlock - An interest rate swap future (not an option)
- Basic Fixed Income Derivative Hedging - Article on Financial-edu.com.
- Hussman Funds - Freight Trains and Steep Curves
- Interest Rate Swap Calculator
- Historical USD Swap Rates
- "All about money rates in the world: Real estate interest rates", WorldwideInterestRates.com
|
|||||||||||||||||||||||||||||||||||||